Recapitulando...¶
- Observação das características do movimento $\rightarrow$ Cinemática
- Formulação das leis que regem as causas do movimento $\rightarrow$ Leis de Newton.
- Conclusão até agora: forças causam o movimento.
- E qual a causa das forças?
- R.: quebramos os objetos em pedaços cada vez menores para ver o que acontece!
- Leitura complementar de Nussenszveig e Feynman extremamente recomendadas.
Gravitação Newtoniana¶
- Observação experimental: matéria atrai matéria. Ex.: experimento de Cavendish.
- Campo gravitacional: quantifica a influência gravitacional de uma massa em suas vizinhanças.
- Sempre atrativa. Propriedades de rotação?
- Força gravitacional: $$\vec{F}_{12}=G\frac{m_1m_2}{r_{12}^2}\hat{r}_{12},$$ onde $m_1, m_2\geq 0$, e $\hat{r}_{12}$ é um vetor unitário na direção da massa 2, partindo da massa 1.
- Constante da gravitação: $G = 6.67408(31)\times 10^{−11}\text{ N m}^2\text{/kg}^2$.
- $G$ é "muito pequeno" e de difícil mensuração.
- Efeitos gravitacionais são muito importantes na escala astronômica.
Gravitação em tempos mais recentes¶
- Questão relevante: não é possível diferenciar um referencial acelerado de uma região sob influência da gravidade. (Einstein).
- Exemplo do elevador na aula anterior!
- Relatividade Geral: campo gravitacional está relacionado a deformações no espaço-tempo.
Colisão entre 2 buracos negros

Primeira detecção de ondas gravitacionais (LIGO 2016)

Eletricidade¶
- Observação: algumas partículas possuem uma carga elétrica $q$. $q$ possui magnitude e sinal. Unidade: ('C': Coulomb)
- Campo elétrico: quantifica a influência elétrica de uma carga em suas vizinhanças.
- Atrativa para sinais opostos, repulsiva para sinais iguais.
- Força elétrica: $$\vec{F}_{12}=\frac{1}{4\pi\epsilon_0}\frac{q_1q_2}{r_{12}^2}\hat{r}_{12},$$ onde $q_1$ e $q_2$ são as cargas elétricas envolvidas, e $\hat{r}_{12}$ é um vetor unitário na direção da carga 2, partindo da carga 1.
- Constante da eletrostática: $k = \frac{1}{4\pi\epsilon_0} \approx 9\times 10^{9}\text{ N m}^2\text{/C}^2$.
- $k$ é "grande", e definido em termos da velocidade da luz.
- Se a força elétrica é "grande", por que em geral não a usamos explicitamente em mecânica?
- R.: objetos usuais costumam ter um balanceamento das cargas elétricas.
Eletromagnetismo (J. C. Maxwell)¶
- Observação: cargas elétricas em movimento possuem uma interação adicional$\rightarrow$Magnetismo.
- Primeira unificação de forças em física (eletricidade e magnetismo).
- Neste caso, a 3ª lei de Newton nem sempre vale: $\vec{F}_{12}\neq\vec{F}_{21}$ em geral.
- Necessário incluir o momento linear dos campos eletromagnéticos
Cauda de cometas (Kepler, 1619)

Pinças ópticas (Ashkin, 1970)

Muito utilizado em biologia. Ex. acima - Estudo de HIV.
Interação forte¶
- Observação: se o núcleo atômico é composto apenas de cargas positivas e neutras, como a repulsão eletrostática não faz o núcleo "estourar"?
- R.: existe outra força "mais forte".
- Interação de curto alcance, só atua nas proximidades do núcleo. Alcance típico: $1\text{ F}$(Fermi)= $10^{-15}\text{ m}$.
- Cromodinâmica quântica (teoria quântica de campos)
- Prêmio Nobel em 2004: David J. Gross, H. David Politzer e Frank Wilczek.

Interação fraca¶
- Interação mais fraca que a forte e a eletromagnética. Também possui um alcance menor.
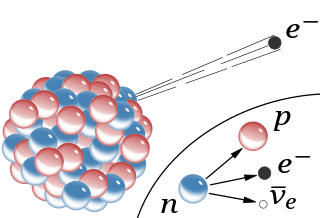
- Importante na compreensão de processos como decaimento $\beta$ (emissão de elétrons por processos de decaimento nucleares).
- Viola a conservação de paridade (simetria de espelho).
- Unificação com o eletromagnetismo: teoria eletrofraca (teoria quântica de campos).
- Prêmio Nobel em 1979: Sheldon Lee Glashow, Abdus Salam e Steven Weinberg.
Visão geral¶
| Força | Intensidade relativa da força | Descrição quântica |
|---|---|---|
| Forte | 1 | Sim |
| Eletromagnética | $10^{-2}$ | Sim |
| Fraca | $10^{-7}$ | Sim |
| Gravitacional | $10^{-38}$ | Não |
- Modelo padrão produz uma descrição quântica unificada para todas as forças conhecidas, exceto a gravidade. A unificação é possível?
- Em sistemas mecânicos simples, precisamos apenas das forças gravitacional e eletromagnética.
- Exemplo de interação gravitacional: objetos com a terra.
- Exemplo de interação eletromagnética: objetos com outros objetos.
Atrito, tração, forças elásticas... são forças derivadas das interações eletromagnéticas microscópicas entre os átomos e moléculas do sistema considerado.
Atrito entre superfícies secas¶
- $F_e$: Atrito estático entre superfícies em repouso relativo.
- $F_{e,max}=\mu_eN$: Maior valor para a força devido ao atrito estático.
- $F_{c}=\mu_cN$: Atrito cinético entre superfícies que possuem movimento relativo.
- Em geral, $F_c\leq F_{e,max}$.
subplot(121)
ax = plt.gca(); ax.set_aspect('equal')
axis("off")
# Desenhar sup horizontal
height = 1
width = 4
c1 = vector2D(origin=(-width/4,-height),dxdy=(width,0))
c2 = vector2D(origin=c1.origin, dxdy=(0,height))
c3 = vector2D(origin=c2.tip, dxdy=c1.dxdy)
c4 = vector2D(origin=c1.origin, dxdy=c1.dxdy)
fill_between_vector2D([c1,c2,c3,c4], color="brown", alpha=0.5)
# Desenhar um quadrado
side = 2 # lados do quadrado
c1 = vector2D(dxdy=(side,0))
c2 = vector2D(origin=c1.origin, dxdy=(0,side))
c3 = vector2D(origin=c2.tip, dxdy=c1.dxdy)
c4 = vector2D(origin=c1.origin, dxdy=c1.dxdy)
fill_between_vector2D([c1,c2,c3,c4], color="green", alpha=0.5)
# Desenhar vetores normal e peso
square_center = c1.origin + (c1.dxdy+c2.dxdy)/2
offset = array([0, 0.3])
peso = vector2D(origin=square_center-offset, dxdy=(0, -2), label=r"$\vec{P}=m\vec{g}$")
peso.plot(ax); peso.plot_label(ax, relative_position=0.6, distance=0.2)
normal = vector2D(origin=square_center+offset, dxdy=(0, 2), label=r"$\vec{N}$")
normal.plot(ax); normal.plot_label(ax, relative_position=0.2, distance=-0.2)
# Desenhar vetores F e Fat
offset = array([-0.3, 0])
Force = vector2D(origin=square_center-offset, dxdy=(1, 0), label=r"$\vec{F}$")
Force.plot(ax); Force.plot_label(ax, relative_position=0.6, distance=0.2)
Fat = vector2D(origin=square_center+offset, dxdy=(-1, 0), label=r"$\vec{F}_{at}$")
Fat.plot(ax); Fat.plot_label(ax, relative_position=0.6, distance=-0.2)
ylim(-2,4)
subplot(122)
f = array([0,1,1,3])
fat = array([0,1,0.7,0.7])
xlabel(r'$F$'); ylabel(r'$F_{at}$')
xticks([0, 0.4, 1], ['0', r'$F$', r'$F_{e,max}$'])
yticks([0, 0.4, 0.7, 1], ['0', r'$F_{at}=F_e=F$', r'$F_{c}$', r'$F_{e,max}$'])
grid(linestyle='--')
plot(f,fat)
tight_layout()
Atrito entre superfícies secas¶
- A força de atrito é sempre oposta a direção do movimento
- $\mu_e$ e $\mu_c$ dependem apenas das superfícies de contato.
- Quando as superfícies se movimentam, $F_{at} = \mu_c N$.
- Quando $F\leq F_{e,max}$ e o sistema estiver parado, $F_e=F$.
- Apenas na iminência do deslizamento que $$F=F_{e,max}$$
Exemplos¶
6a Questão (1EE-2017.1): Dois blocos estão ligados por uma corda que passa por uma polia de massa desprezível e sem atrito em seu eixo, como mostra a figura ao lado. O bloco A tem massa $m_A = 2$ kg e os coeficientes de atrito estático e cinético entre A e a rampa são respectivamente $\mu_e = 1/2 = 0, 5$ e $\mu_c = 1/3 = 0, 33...$
Considere que os corpos s~ao liberados a partir do repouso, $g = 10$ m/s$^2$, $\sin\theta = 0, 8$ e $\cos\theta = 0, 6$.
(a) Determine a menor massa possível do bloco B acima da qual o bloco A sobe a rampa.
(b) Determine a maior massa possível do bloco B abaixo da qual o bloco A desce a rampa.
(c) Obtenha a aceleração do bloco A quando a massa de B é $m_B=3$kg, indicando o módulo, direção e sentido.
Força de arrasto e velocidade terminal¶
- Força de oposição ao movimento devido à um fluido (Ex.: ar, água...)
- Força de arrasto $\vec{D}$: Direção igual à do movimento, e sentido oposto (similar à $\vec{F}_{at}$)
- $\vec{D}$ depende da velocidade $v$ do objeto
- Experimentalmente, seu módulo $$D = \frac{1}{2}C\rho A v^2$$$C$: Coeficiente de arrasto$\rho$: Densidade do fluido$A$: Área transversal (área perpendicular à $\vec{v}$)$v$: módulo da velocidade
Coeficiente de arrasto $C$¶
- Tipicamente, $C$ varia entre $0,4$ e $1,0$.
- Depende fortemente da geometria.
- Qual dos objetos abaixo deve ter um menor coeficiente de arrasto? (Supor que $A$ é igual para ambos).
Bola de futebol

Caixa

- R.: Bola é mais "aerodinâmica". Seu valor de $C$ é menor.
Área transversal $A$¶
- Quanto maior a área transversal, maior o arrasto produzido pelo fluido.
- Qual dos esquiadores abaixo percebe menor arrasto?
Esquiador 1

Esquiador 2

- R.: Esquiador 2, pois sua área transversal é menor.
Velocidade terminal¶
- Suponha um objeto em queda sob ação do peso $P$, partindo do repouso. (Ex.: gota de chuva, paraquedista)
- $$ D - P = ma $$
- Inicialmente, $v=0$, logo $D=0$.
- Devido a $P$, $v$ aumenta, e consequentemente $D$ também aumenta ($D\propto v^2$).
- Qual o maior valor para $D$? $D$ é uma força que resiste ao movimento! (similar ao atrito).
- $D-P=0$, ou $$D=\frac{1}{2}C\rho A v^2=P.$$
- Neste caso, $v=v_t\equiv$ velocidade terminal, $$v_t=\sqrt{\frac{2P}{C\rho A}}.$$
- Algumas velocidades terminais no ar (adaptado da tab. 6-1 do livro)
| Objeto | Velocidade Terminal (m/s) | Distância(*) para 95% (m) |
|---|---|---|
| Peso (usado no arremesso de peso) | 145 | 2500 |
| Paraquedista em queda livre (típico) | 60 | 430 |
| Bola de beisebol | 42 | 210 |
| Bola de tênis | 31 | 115 |
| Bola de basquete | 20 | 47 |
| Bola de pingue-pongue | 9 | 10 |
| Gota de chuva (raio = 1,5 mm) | 7 | 6 |
| Paraquedista (típico) | 5 | 3 |
(*) Distância da queda necessária para atingir 95% da velocidade terminal.
Exemplo (Livro)¶
Uma gota de chuva de raio $R = 1,5\text{ mm}$ cai de uma nuvem que está a uma altura $h = 1200\text{ m}$ acima do solo. O coeficiente de arasto $C$ da gota é $0,60$. Suponha que a gota permanece esférica durante toda a queda. A massa específica da água é $\rho_a=1000\text{ kg/m}^3$ e a massa especfica do ar é $\rho_ar=1,2\text{ kg/m}^3$.
- (a) De acordo com a Tabela anterior, a gota atinge a velocidade terminal depois de cair apenas alguns metros. Qual é a velocidade terminal?
- (b) Qual seria a velocidade da gota imediatamente antes do impacto com o chão se não existisse a força de arasto?
Exemplo (M. Copelli)¶
A figura mostra dois submarinos idênticos, A e B, que se movem com a mesma velocidade $v$. Eles transportam objetos cônicos maciços idênticos, porém orientados diferentemente (vide figura). Nesta situação, qual motor exerce a maior força?
from IPython.display import Image, display
Image(filename="C6/dois-submarinos.png")
- A
- B
- Ambos exercem a mesma força
- Não é possível determinar a partir dos dados do problema
Movimento circular uniforme (MCU)¶
- No MCU, $a_{cpt}=\frac{v^2}{r}$ tem direção radial, apontando para dentro do círculo.
- Força centrípeta $F_{cpt} = m a_{cpt}=m \frac{v^2}{r}$.- Força resultante associada ao MCU- NÃO é um novo tipo de força- Fisicamente, $F_{cpt}$ é o resultado da ação de outras forças.
- Carro em uma trajetória curva $\rightarrow$ $F_{cpt}$ devido ao atrito.
- Pedra girando horizontalmente, presa por um fio $\rightarrow$ $F_{cpt}$ devido à tração.
- Satélite em órbita em torno da terra $\rightarrow$ $F_{cpt}$ devido ao peso.
ax = plt.axes()
# Círculo
theta = linspace(0,2*pi,100)
radius = 1
theta0 = 0.5
x = radius*cos(theta+theta0)
y = radius*sin(theta+theta0)
plot(x,y, 'k:')
plot([x[0]], [y[0]], 'ro')
# Vetores velocidade
v = vector2D(origin=[x[0],y[0]], label=r'$\vec{v}$', mpl_options=uvector_style)
v.polar = (0.5, theta0+pi/2)
v.plot(ax); v.plot_label(ax, distance=-0.0)
# Vetor aceleração
r = vector2D(origin=[x[0],y[0]], label=r'$\vec{a}(t)$', mpl_options=avector_style)
r.polar= (0.75, theta0+pi)
r.plot(ax); r.plot_label(ax, distance=0.15)
axis('off'); ax.set_aspect('equal')
Exemplo¶
Um carro de massa $m$ dá voltas de raio $r$ com velocidade escalar constante numa pista horizontal (vide figura). A pista exerce uma força normal de módulo $N$ sobre o carro. Qual deve ser o atrito entre os pneus e a pista para que o carro realize a trajetória circular?
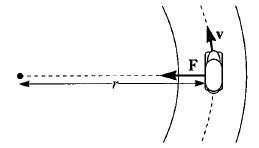
- R.: $F_{at}=m \frac{v^2}{r}$
Exemplo (M. Copelli)¶
Um carro de massa $m$ dá voltas de raio $r$ com velocidade escalar constante numa pista inclinada de um ângulo $\theta$ (vide figura). A pista exerce uma força normal de módulo $N$ sobre o carro. Suponha que não exista atrito nenhum na pista. Neste caso, a força centrípeta é:
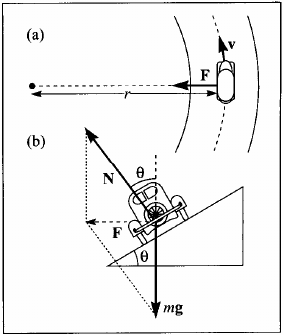
- $N$
- $N - mg\cos\theta$
- $N\sin\theta$
- $mg\cos\theta$
Exemplo (M. Copelli)¶
Um motociclista dá voltas num globo da morte (vide figura) em movimento circular uniforme de raio $R$. O módulo da força peso da moto + motociclista é $P$. O módulo da força normal exercida pelo globo é $N$, podendo variar ao longo do percurso. No ponto A da trajetória, o módulo da força centrípeta $F_c$ é:
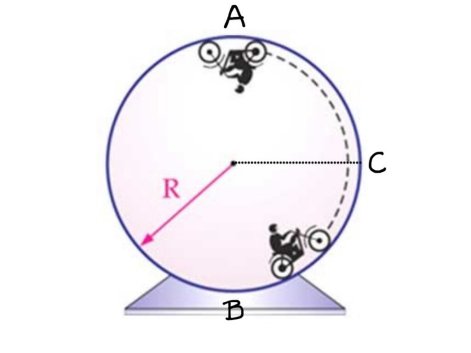
- $F_c = 0$
- $F_c = P+N $
- $F_c = P$
- $F_c = P - N$
Questão 3 - 2017.1¶
Um disco está preso a um fio cujo comprimento é $0,5\text{ m}$, e realiza um movimento circular sobre uma mesa de altura $0,8\text{ m}$ em relação ao solo. O fio arrebenta e o disco é lançado horizontalmente, atingindo o solo após um deslocamento horizontal de $2\text{ m}$. Qual aceleração centrípeta do disco antes de o fio arrebentar? Despreze o atrito entre o disco e a mesa e use que $g=10\text{ m/s}^2$.
R.: 50 m/s$^2$
Questão 4 - 2016.2¶
A figura ao lado mostra um sistema composto por duas partículas, ambas com massa $m = 0,50\text{ kg}$, conectadas por fios inextensíveis e de massas desprezíveis de comprimento $L = 0,30\text{ m}$ cada. O fio 1 está preso ao ponto fixo $P$, enquanto o fio 2 liga uma partícula à outra. O sistema gira em torno do ponto $P$ sobre uma superfície plana horizontal sem atrito, com velocidade angular $\omega = 2,0 \text{ rad/s}$. Os módulos das velocidades $\vec v_1$ e $\vec v_2$ de cada partícula são constantes. $\vec T_1$ e $\vec T_2$ são as trações nos fios 1 e 2 respectivamente.
| (a) $T_1 = 20\text{ N}$ e $T_2 = 6,7\text{ N}$ | (b) $T_1 = 2,4\text{ N}$ e $T_2 = 1,2\text{ N}$ | (c) $T_1 = 1,2\text{ N}$ e $T_2 = 2,4\text{ N}$ |
|---|---|---|
| (d) $T_1 = 1,8\text{ N}$ e $T_2 = 1,2\text{ N}$ | (e) $T_1 = 1,8\text{ N}$ e $T_2 = 0,6\text{ N}$ | (f) $T_1 = 0,6\text{ N}$ e $T_2 = 1,2\text{ N}$ |
| (g) $T_1 = T_2 = 6,7\text{ N}$ | (h) $T_1 = 6,7\text{ N}$ e $T_2 = 20\text{ N}$ | (i) $T_1=T_2=0.6\text{ N}$ |
R.: (d)


